7. 相关性分析

前面的假设检验、方差分析基本上都是围绕差异性分析，不论是单个总体还是两个总体及以上，总之都是属于研究“区别”，从本节开始，我们关注“联系”，变量之间的关系分为 函数关系和相关关系。 本节这里重点探讨的是不同类型变量之间的相关性，千万记住一点相关性不代表因果性。除表中列出的常用方法外，还有Tetrachoric、相关系数等。

连续型变量 vs 连续型变量 : Pearson / Spearmanr

Pearson

Pearson相关系数度量了两个连续变量之间的线性相关程度；

import random 
import numpy as np
import pandas as pd

np.random.seed(10)
df = pd.DataFrame({'商品曝光量':[1233,1333,1330,1323,1323,1142,1231,1312,1233,1123],
     '购买转化率':[0.033,0.034,0.035,0.033,0.034,0.029,0.032,0.034,0.033,0.031]})
df

• Pandas计算Pearson相关系数

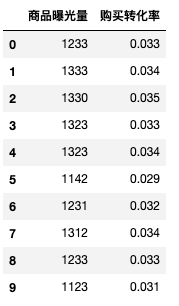
pd.Series.corr(df['商品曝光量'], df['购买转化率'],method = 'pearson') # pearson相关系数
# 0.885789300493948

• scipy计算Pearson相关系数

import scipy.stats as stats

# 假设有两个变量X和Y
X = df['商品曝光量']
Y = df['购买转化率']

# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.pearsonr(X, Y)

print("Pearson相关系数:", corr)
print("p值:", p_value)
# Pearson相关系数: 0.8857893004939478
# p值: 0.0006471519603654732

Spearman等级相关系数

Spearman等级相关系数可以衡量非线性关系变量间的相关系数，是一种非参数的统计方法，可以用于定序变量或不满足正态分布假设的等间隔数据；

import random 
import numpy as np
import pandas as pd

np.random.seed(10)
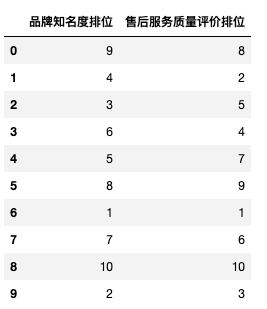
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
     '售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df

• Pandas计算spearman相关系数

pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'spearman') # spearman秩相关
# 0.8787878787878788

• scipy计算spearman相关系数

import scipy.stats as stats

# 假设有两个变量X和Y
X = df['品牌知名度排位']
Y = df['售后服务质量评价排位']

# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.spearmanr(X, Y)

print("斯皮尔曼相关系数:", corr)
print("p值:", p_value)
# 斯皮尔曼相关系数: 0.8787878787878788
# p值: 0.0008138621117322101

结论:p = 0.0008＜0.05，表明两变量之间的正向关系很显著。

二分类变量（自然）vs 连续型变量 :Point-biserial

假设我们想要研究性别对于某种疾病是否存在影响。我们有一个二元变量“性别”（男、女）和一个连续型变量“疾病指数”。我们想要计算性别与疾病指数之间的相关系数，就需要用到Point-biserial相关系数。

import scipy.stats as stats

# 创建一个列表来存储数据
gender = [0, 1, 0, 1, 1, 0]
disease_index = [3.2, 4.5, 2.8, 4.0, 3.9, 3.1]

# 使用pointbiserialr函数计算Point-biserial相关系数和p值
corr, p_value = stats.pointbiserialr(gender, disease_index)

print("Point-biserial相关系数:", corr)
print("p值:", p_value)
# Point-biserial相关系数: 0.9278305692406299
# p值: 0.007624695507848026

结论:p = 0.007＜0.05，表明两变量之间的正向关系很显著。即性别与疾病指数正相关

无序分类变量 vs 连续型变量 ： ANOVA

假设我们想要比较不同教育水平的学生在CDA考试成绩上是否存在显著差异。我们有一个无序分类变量“教育水平”（高中、本科、研究生）和一个连续型变量“考试成绩”。

import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

# 创建一个DataFrame来存储数据
data = pd.DataFrame({
    '教育水平': ['高中', '本科', '本科', '研究生', '高中', '本科', '研究生'],
    '考试成绩': [80, 90, 85, 95, 75, 88, 92]
})

# 使用ols函数创建一个线性模型
model = ols('考试成绩 ~ C(教育水平)', data=data).fit()

# 使用anova_lm函数进行方差分析
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table

结论:p = 0.0102＜0.05，拒绝原假设，表明两变量之间的正向关系很显著。教育水平与考试成绩正相关

有序分类变量 vs 连续型变量

将连续型变量离散化后当做有序分类，然后用 有序分类变量 VS 有序分类变量的方法

二分类变量 vs 二分类变量 ：检验 联合 Cramer's V

一项研究调查了不同性别的成年人对在公众场合吸烟的态度，结果如表所示。那么，性别与对待吸烟的态度之间的相关程度

import numpy as np
from scipy.stats import chi2_contingency

observed = np.array([[15, 10],
                     [10, 26]])
observed

chi2, p, dof, expected = chi2_contingency(observed,correction =False) # correction =False
# 卡方值 
# P值 
# 自由度： 
# 与原数据数组同维度的对应期望值

chi2, p
#(6.3334567901234555, 0.011848116168529757)

结论:p = 0.0118＜0.05，拒绝原假设，表明两变量之间的正向关系很显著。

phi = np.sqrt(chi2/n)
print("phi's V:", phi)
# phi's V: 0.3222222222222222

卡方检验时有多种指标可表示效应量，可结合数据类型及交叉表格类型综合选择

• 第一：如果是2*2表格，建议使用 指标
• 第二：如果是33,或 44表格，建议使用列联系数；
• 第三：如果是n*n(n>4)表格，建议使用 校正列联系数；
• 第四：如果是m*n(m不等于n)表格，建议使用 Cramer V指标；
• 第五：如果X或Y中有定序数据，建议使用 指标；

这里只列出 指标 和 Cramer V指标 的计算，其他计算方式请读者自行研究。

# 计算Cramer's V
contingency_table = observed
n = contingency_table.sum().sum()
phi_corr = np.sqrt(chi2 / (n * min(contingency_table.shape) - 1))
v = phi_corr / np.sqrt(min(contingency_table.shape) - 1)

print("Cramer's V:", v)
# Cramer's V: 0.22878509151645754

二分类变量（有序） 连续型变量： Biserial

import numpy as np
from scipy.stats import pearsonr

# 生成随机的二元变量
binary_variable = np.random.choice([0, 1], size=100)

# 生成随机的连续变量
continuous_variable = np.random.normal(loc=0, scale=1, size=100)


# 注：此处的代码未经严格考证，请谨慎使用
def biserial_correlation(binary_variable, continuous_variable):
    binary_variable_bool = binary_variable.astype(bool)
    binary_mean = np.mean(binary_variable_bool)
    binary_std = np.std(binary_variable_bool)
    
    binary_variable_norm = (binary_variable_bool - binary_mean) / binary_std
    
    corr, _ = pearsonr(binary_variable_norm, continuous_variable)
    biserial_corr = corr * (np.std(continuous_variable) / binary_std)
    
    return biserial_corr

# 计算Biserial相关系数
biserial_corr = biserial_correlation(binary_variable, continuous_variable)

print("Biserial相关系数:", biserial_corr)
Biserial相关系数: -0.2061772328681707

无序分类变量 vs 无序分类变量

参考 检验

有序分类变量 vs 无序分类变量

参考 检验

有序分类变量 vs 有序分类变量

Kendall秩相关系数

Kendall秩相关系数也是一种非参数的等级相关度量，类似于Spearman等级相关系数。

import random 
import numpy as np
import pandas as pd

np.random.seed(10)
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
     '售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df

pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'kendall') # Kendall Tau相关系数
# 0.7333333333333333

from scipy.stats import kendalltau

# 两个样本数据
x = df['品牌知名度排位']
y = df['售后服务质量评价排位']

# 计算Kendall Tau相关系数
correlation, p_value = kendalltau(x, y)

print("Kendall Tau相关系数:", correlation)
print("p值:", p_value)
# Kendall Tau相关系数: 0.7333333333333333
# p值: 0.002212852733686067

浮生皆纵，恍如一梦，让我们只争朝夕,不负韶华！

下期将为大家带来《统计学极简入门》之 再看t检验、F检验、检验

推荐学习书籍

《CDA一级教材》适合CDA一级考生备考，也适合业务及数据分析岗位的从业者提升自我。完整电子版已上线CDA网校，累计已有10万+在读~

免费加入阅读：https://edu.cda.cn/goods/show/3151?targetId=5147&preview=0