矩阵分解在推荐系统中的应用：NMF和经典SVD实战

数据 

关于NMF，在隐语义模型和NMF（非负矩阵分解）已经有过介绍。

用户和物品的主题分布

运行后输出：

可视化物品的主题分布：

结果：

从距离的角度来看，item 5和item 6比较类似；从余弦相似度角度看，item 2、5、6 比较相似，item 1、3比较相似。

可视化用户的主题分布：

结果：

从距离的角度来看，Fred、Ben、Tom的口味差不多；从余弦相似度角度看，Fred、Ben、Tom的口味还是差不多。

如何推荐

现在对于用户A，如何向其推荐物品呢？

方法1： 找出与用户A最相似的用户B，将B评分过的、评分较高、A没评分过的的若干物品推荐给A。

方法2： 找出用户A评分较高的若干物品，找出与这些物品相似的、且A没评分的若干物品推荐给A。

方法3： 找出用户A最感兴趣的k个主题，找出最符合这k个主题的、且A没评分的若干物品推荐给A。

方法4： 由NMF得到的两个矩阵，重建评分矩阵。例如：

运行结果：

对于Tom（评分矩阵的第2行），其未评分过的物品是item 2、item 3、item 4。item 2的推荐值是2.19148602，item 3的推荐值是1.73560797，item 4的推荐值是0，若要推荐一个物品，推荐item 2。

如何处理有评分记录的新用户

NMF是将非负矩阵V分解为两个非负矩阵W和H：

V=W×H

在本文上面的实现中，V对应评分矩阵，W是用户的主题分布，H是物品的主题分布。

对于有评分记录的新用户，如何得到其主题分布？

方法1： 有评分记录的新用户的评分数据放入评分矩阵中，使用NMF处理新的评分矩阵。

方法2： 物品的主题分布矩阵H保持不变，将V更换为新用户的评分组成的行向量，求W即可。

下面尝试一下方法2。

设新用户Bob的评分记录为：

运行结果是：

经典SVD

关于SVD的一篇好文章：强大的矩阵奇异值分解(SVD)及其应用。

相关分析与上面类似，这里就直接上代码了。

运行结果：

可视化一下：

经典SVD + 协同过滤

0代表没有评分，但是上面的方法（如何推荐这一节的方法4）又确实把0看作了评分，所以最终得到的只是一个推荐值（而且总体都偏小），而无法当作预测的评分。在How do I use the SVD in collaborative filtering?有这方面的讨论。

SVD简要介绍

SVD的目标是将m*n大小的矩阵A分解为三个矩阵的乘积：

[latex]
A = U S V^{T}
[/latex]

U和V都是正交矩阵，大小分别是m*m、n*n。S是一个对角矩阵，大小是m*n，对角线存放着奇异值，从左上到右下依次减小，设奇异值的数量是r。

取k，k<<r。

取得UU的前k列得到UkUk，SS的前k个奇异值对应的方形矩阵得到SkSk，VTVT的前k行得到VTkVkT，于是有

[latex]
A_{k} = U_{k} S_{k} V^{T}_{k}
[/latex]

AkAk可以认为是AA的近似。

下面的算法将协同过滤和SVD结合了起来。

Item-based Filtering Enhanced by SVD

这个算法来自下面这篇论文：

Vozalis M G, Margaritis K G. Applying SVD on Generalized Item-based Filtering[J]. IJCSA, 2006, 3(3): 27-51.

1、 设评分矩阵为R，大小为m*n，m个用户，n个物品。R中元素rijrij代表着用户uiui对物品ijij的评分。

2、 预处理R，消除掉其中未评分数据（即值为0）的评分。

计算R中每一行的平均值（平均值的计算中不包括值为0的评分），令Rfilled−in=RRfilled−in=R，然后将Rfilled−inRfilled−in中的0设置为该行的平均值。

计算R中每一列的平均值（平均值的计算中不包括值为0的评分）riri，Rfilled−inRfilled−in中的所有元素减去对应的riri，得到正规化的矩阵RnormRnorm。(norm，即normalized)。

3、 对RnormRnorm进行奇异值分解，得到：
[latex]
R_{norm} = U S V^{T}
[/latex]

4、 设正整数k，取得UU的前k列得到UkUk，SS的前k个奇异值对应的方形矩阵得到SkSk，VTVT的前k行得到VTkVkT，于是有

[latex]
R_{red} = U_{k} S_{k} V^{T}_{k}
[/latex]

red，即dimensionality reduction中的reduction。可以认为k是指最重要的k个主题。定义RredRred中元素rrijrrij用户i对物品j在矩阵RredRred中的值。

5、 [latex] U_{k} S_{k}^{\frac{1}{2}}[/latex]，是用户相关的降维后的数据，其中的每行代表着对应用户在新特征空间下位置。[latex] S_{k}^{\frac{1}{2}}V^{T}_{k}[/latex]，是物品相关的降维后的数据，其中的每列代表着对应物品在新特征空间下的位置。

S12k∗VTkSk12∗VkT中的元素mrijmrij代表物品j在新空间下维度i中的值，也可以认为是物品j属于主题i的程度。（共有k个主题）。

6、 获取物品之间相似度。

根据S12k∗VTkSk12∗VkT计算物品之间的相似度，例如使用余弦相似度计算物品j和f的相似度：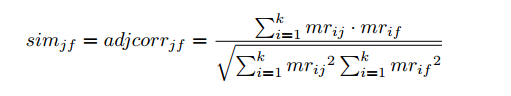

相似度计算出来后就可以得到每个物品最相似的若干物品了。

7、 使用下面的公式预测用户a对物品j的评分：

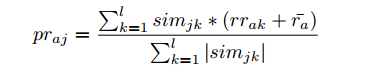
这个公式里有些变量的使用和上面的冲突了（例如k）。
ll是指取物品j最相似的ll个物品。
mrijmrij代表物品j在新空间下维度i中的值，也可以认为是物品j属于主题i的程度。
simjksimjk是物品j和物品k的相似度。
RredRred中元素rrakrrak是用户a对物品k在矩阵RredRred中对应的评分。ra¯ra¯是指用户a在评分矩阵RR中评分的平均值（平均值的计算中不包括值为0的评分）。