一篇文章透彻解读聚类分析及案例实操(二)

4  SAS聚类分析案例

1 问题背景

考虑下面案例，一个棒球管理员希望根据队员们的兴趣相似性将他们进行分组。显然，在该例子中，没有响应变量。管理者希望能够方便地识别出队员的分组情况。同时，他也希望了解不同组之间队员之间的差异性。

该案例的数据集是在SAMPSIO库中的DMABASE数据集。下面是数据集中的主要的变量的描述信息：

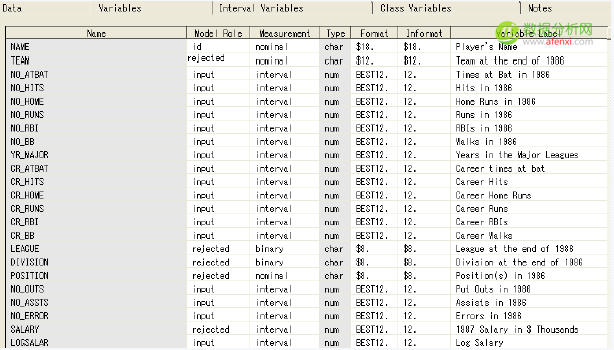
在这个案例中，设置TEAM，POSITION，LEAGUE，DIVISION和SALARY变量的模型角色为rejected，设置SALARY变量的 模型角色为rejected是由于它的信息已经存储在LOGSALAR中。在聚类分析和自组织映射图中是不需要目标变量的。如果需要在一个目标变量上识别 分组，可以考虑预测建模技术或者定义一个分类目标。

2 聚类方法概述

聚类分析经常和有监督分类相混淆，有监督分类是为定义的分类响应变量预测分组或者类别关系。而聚类分析，从另一方面考虑，它是一种无监督分类技术。 它能够在所有输入变量的基础上识别出数据集中的分组和类别信息。这些组、簇，赋予不同的数字。然而，聚类数目不能用来评价类别之间的近似关系。自组织映射 图尝试创建聚类，并且在一个图上用图形化的方式绘制出聚类信息，在此处我们并没有考虑。

1) 建立初始数据流

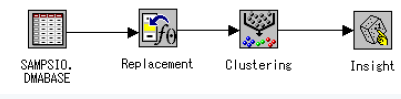
2) 设置输入数据源结点

打开输入数据源结点

从SAMPSIO库中选择DMABASE数据集

设置NAME变量的模型角色为id，TEAM，POSIOTION，LEAGUE，DIVISION和SALARY变量的模型角色为rejected

探索变量的分布和描述性统计信息

选择区间变量选项卡，可以观察到只有LOGSALAR和SALARY变量有缺失值。选择类别变量选项卡，可以观察到没有缺失值。在本例中，没有涉及到任何类别变量。

关闭输入数据源结点，并保存信息。

3) 设置替代结点

虽然并不是总是要处理缺失值，但是有时候缺失值的数量会影响聚类结点产生的聚类解决方案。为了产生初始聚类，聚类结点往往需要一些完整的观测值。当缺失值太多的时候，需要用替代结点来处理。虽然这并不是必须的，但是在本例中使用到了。

4) 设置聚类结点

打开聚类结点，激活变量选项卡。K-means聚类对输入数据是敏感的。一般情况下，考虑对数据集进行标准化处理。

在变量选项卡，选择标准偏差单选框

选择聚类选项卡

观察到默认选择聚类数目的方法是自动的

关闭聚类结点

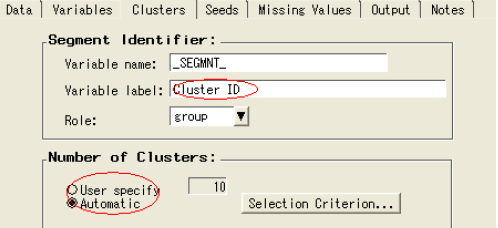
5) 聚类结果

在聚类结点处运行流程图，查看聚类结果。

6) 限定聚类数目

打开聚类结点

选择聚类选项卡

在聚类数目选择部分，点击选择标准按钮

输入最大聚类数目为10

点击ok，关闭聚类结点

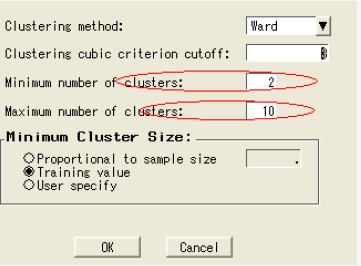
7)结果解释

我们可以定义每个类别的信息，结合背景识别每个类型的特征。选择箭头按钮，

选择三维聚类图的某一类别，

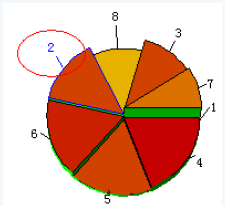
在工具栏选择刷新输入均值图图标，

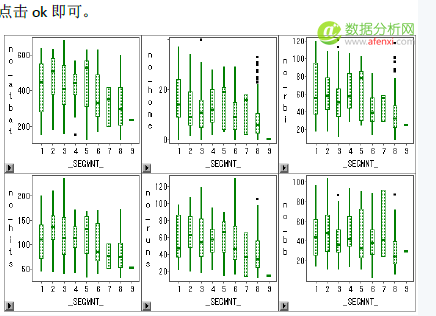
点击该图标，可以查看该类别的规范化均值图

同理，可以根据该方法对其他类别进行解释。

8)运用Insight结点

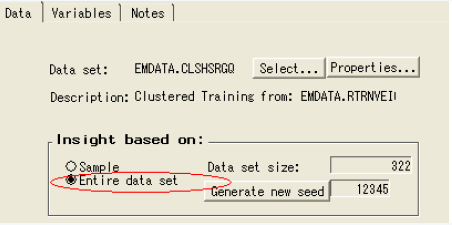
Insight结点可以用来比较不同属性之间的异常。打开insight结点，选择整个数据集，关闭结点。

从insight结点处运行。

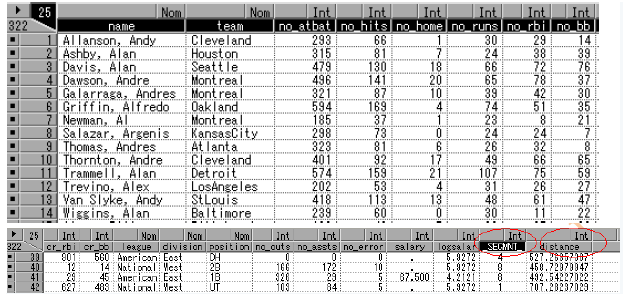
变量_SEGMNT_标识类别，distance标识观测值到所在类别中心的距离。运用insight窗口的analyze工具评估和比较聚类结果。

首先把_SEGMNT_的度量方式从interval转换成nominal。

R语言篇

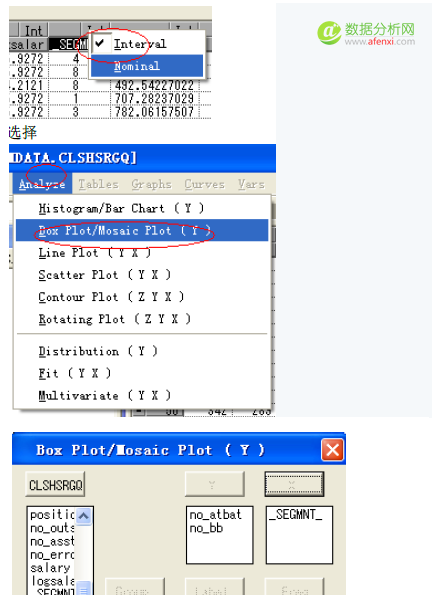
以R基础包自带的鸢尾花(Iris)数据进行聚类分析。分析代码如下：

###### 代码清单 #######

data(iris); attach(iris)

iris.hc <- hclust( dist(iris[,1:4]))

# plot( iris.hc, hang = -1)

plclust( iris.hc, labels = FALSE, hang = -1)

re <- rect.hclust(iris.hc, k = 3)

iris.id <- cutree(iris.hc, 3)

table(iris.id, Species)

###### 运行结果 #######

> table(iris.id,Species)

Species

iris.id setosa versicolor virginica

1 50 0 0

2 0 23 49

3 0 27 1

聚类分析生成的图形如下：

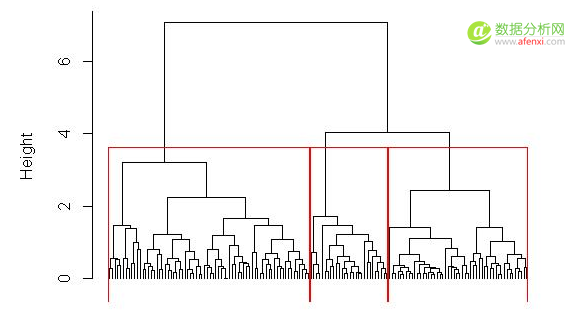
结果表明，函数cuttree()将数据iris分类结果iris.hc编为三组分别以1,2, 3表示，保存在iris.id中。将iris.id与iris中Species作比较发现：1应该是setosa类，2应该是virginica类(因为 virginica的个数明显多于versicolor)，3是versicolor。

仍以R基础包自带的鸢尾花(Iris)数据进行K-均值聚类分析，分析代码如下：

###### 代码清单 #######

library(fpc)

data(iris)

df<-iris[,c(1:4)]

set.seed(252964) # 设置随机值，为了得到一致结果。

(kmeans <- kmeans(na.omit(df), 3)) # 显示K-均值聚类结果

plotcluster(na.omit(df), kmeans$cluster) # 生成聚类图

生成的图如下：

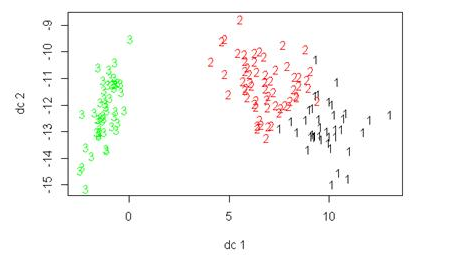
Python篇

Python运行条件：

1.Python运行环境与编辑环境;

2.Matplotlib.pyplot图形库，可用于快速绘制2D图表，与matlab中的plot命令类似，而且用法也基本相同。

# coding=utf-8

##

作者:Chan

程序:kmeans算法

##

import matplotlib.pyplot as plt

import math

import numpy

import random

#dotOringalNum为各个分类最初的大小

dotOringalNum=100

#dotAddNum最后测试点的数目

dotAddNum=1000

fig = plt.figure()

ax = fig.add_subplot(111)

sets=

colors=[‘b’,’g’,’r’,’y’]

#第一个分类，颜色为蓝色，在左下角

a=

txx=0.0

tyy=0.0

for i in range(0,dotOringalNum):

tx=float(random.randint(1000,3000))/100

ty=float(random.randint(1000,3000))/100

a.append([tx,ty])

txx+=tx

tyy+=ty

#ax.plot([tx],[ty],color=colors[0],linestyle=”,marker=’.’)

#a的第一个元素为a的各个元素xy值之合

a.insert(0,[txx,tyy])

sets.append(a)

#第二个分类，颜色为绿色，在右上角

b=

txx=0.0

tyy=0.0

for i in range(0,dotOringalNum):

tx=float(random.randint(4000,6000))/100

ty=float(random.randint(4000,6000))/100

b.append([tx,ty])

txx+=tx

tyy+=ty

#ax.plot([tx],[ty],color=colors[1],linestyle=”,marker=’.’)

b.insert(0,[txx,tyy])

sets.append(b)

#第三个分类，颜色为红色，在左上角

c=

txx=0.0

tyy=0.0

for i in range(0,dotOringalNum):

tx=float(random.randint(1000,3000))/100

ty=float(random.randint(4000,6000))/100

c.append([tx,ty])

txx+=tx

tyy+=ty

#ax.plot([tx],[ty],color=colors[2],linestyle=”,marker=’.’)

c.insert(0,[txx,tyy])

sets.append(c)

#第四个分类，颜色为黄色，在右下角

d=

txx=0

tyy=0

for i in range(0,dotOringalNum):

tx=float(random.randint(4000,6000))/100

ty=float(random.randint(1000,3000))/100

d.append([tx,ty])

txx+=tx

tyy+=ty

#ax.plot([tx],[ty],color=colors[3],linestyle=”,marker=’.’)

d.insert(0,[txx,tyy])

sets.append(d)

#测试

for i in range(0,dotAddNum):

tx=float(random.randint(0,7000))/100

ty=float(random.randint(0,7000))/100

dist=9000.0

setBelong=0

for j in range(0,4):

length=len(sets[j])-1

centX=sets[j][0][0]/length

centY=sets[j][0][1]/length

if (centX-tx)*(centX-tx)+(centY-ty)*(centY-ty)

运行效果: