不平衡数据分类算法介绍与比较

在数据挖掘中，经常会存在不平衡数据的分类问题，比如在异常监控预测中，由于异常就大多数情况下都不会出现，因此想要达到良好的识别效果普通的分类算法还远远不够，这里介绍几种处理不平衡数据的常用方法及对比。

符号表示

记多数类的样本集合为L，少数类的样本集合为S。

用r=|S|/|L|表示少数类与多数类的比例

基准

我们先用一个逻辑斯谛回归作为该实验的基准：

Weighted loss function

一个处理非平衡数据常用的方法就是设置损失函数的权重，使得少数类判别错误的损失大于多数类判别错误的损失。在python的scikit-learn中我们可以使用class_weight参数来设置权重。

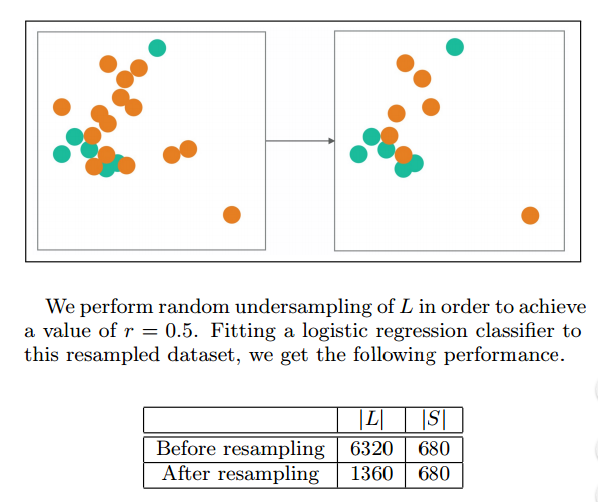
欠采样方法(undersampling)

Random undersampling of majority class

一个最简单的方法就是从多数类中随机抽取样本从而减少多数类样本的数量，使数据达到平衡。

Edited Nearest Neighbor (ENN)

我们将那些L类的样本，如果他的大部分k近邻样本都跟他自己本身的类别不一样，我们就将他删除。

Repeated Edited Nearest Neighbor

这个方法就是不断的重复上述的删除过程，直到无法再删除为止。

Tomek Link Removal

如果有两个不同类别的样本，它们的最近邻都是对方，也就是A的最近邻是B，B的最近邻是A，那么A,B就是Tomek link。我们要做的就是讲所有Tomek link都删除掉。那么一个删除Tomek link的方法就是，将组成Tomek link的两个样本，如果有一个属于多数类样本，就将该多数类样本删除掉。

过采样方法(Oversampling)

我们可以通过欠抽样来减少多数类样本的数量从而达到平衡的目的，同样我们也可以通过，过抽样来增加少数类样本的数量，从而达到平衡的目的。

Random oversampling of minority class

一个最简单的方法，就是通过有放回的抽样，不断的从少数类的抽取样本，不过要注意的是这个方法很容易会导致过拟合。我们通过调整抽样的数量可以控制使得r=0.5

Synthetic Minority Oversampling Technique(SMOTE)

这是一个更为复杂的过抽样方法，他的方法步骤如下：

For each point p in S:
1. Compute its k nearest neighbors in S.
2. Randomly choose r ≤ k of the neighbors (with replacement).
3. Choose a random point along the lines joining p and
each of the r selected neighbors.
4. Add these synthetic points to the dataset with class
S.
For each point p in S：
1. 计算点p在S中的k个最近邻
2. 有放回地随机抽取R≤k个邻居
3. 对这R个点，每一个点与点p可以组成一条直线，然后在这条直线上随机取一个点，就产生了一个新的样本，一共可以这样做从而产生R个新的点。
4.  将这些新的点加入S中

Borderline-SMOTE1

这里介绍两种方法来提升SMOTE的方法。

For each point p in S:
    1. Compute its m nearest neighbors in T. Call this set Mp and let m'= |Mp ∩ L|.
    2. If m'= m, p is a noisy example. Ignore p and continue to the next point.
    3. If 0 ≤ m'≤m/2, p is safe. Ignore p and continue to the next point.
    4. If m/2 ≤ m'≤ m, add p to the set DANGER.
For each point d in DANGER, apply the SMOTE algorithm to generate synthetic examples.
For each point p in S:
    1. 计算点p在训练集T上的m个最近邻。我们称这个集合为Mp然后设 m'= |Mp ∩ L| (表示点p的最近邻中属于L的数量).
    2. If m'= m, p 是一个噪声,不做任何操作.
    3. If 0 ≤m'≤m/2, 则说明p很安全，不做任何操作.
    4. If m/2 ≤ m'≤ m, 那么点p就很危险了，我们需要在这个点附近生成一些新的少数类点，所以我们把它加入到DANGER中.
最后，对于每个在DANGER中的点d，使用SMOTE算法生成新的样本.

我们应用Borderline-SMOTE1的参数设置为k=5,为了使得r=0.5

Borderline-SMOTE2

这个与Borderline-SMOTE1很像，只有最后一步不一样。
在DANGER集中的点不仅从S集中求最近邻并生成新的少数类点，而且在L集中求最近邻，并生成新的少数类点，这会使得少数类的点更加接近其真实值。

FORpinDANGER:1.在S和L中分别得到k个最近邻样本Sk和Lk。2.在Sk中选出α比例的样本点和p作随机的线性插值产生新的少数类样本3.在Lk中选出1−α比例的样本点和p作随机的线性插值产生新的少数类样本。

为了达到r=0.5 实验取k=5

组合方法(Combination)

SMOTE + Tomek Link Removal

SMOTE + ENN

集成方法(Ensemble)

EasyEnsemble

一个最简单的集成方法就是不断从多数类中抽取样本，使得每个模型的多数类样本数量和少数类样本数量都相同，最后将这些模型集成起来。
算法伪代码如下：

1. For i = 1, ..., N:
    (a) 随机从 L中抽取样本Li使得|Li| = |S|.
    (b) 使用Li和S数据集，训练AdaBoost分类器Fi。



2. 将上述分类器联合起来

BalanceCascad

这个方法跟EasyEnsemble有点像，但不同的是，每次训练adaboost后都会扔掉已被正确分类的样本，经过不断地扔掉样本后，数据就会逐渐平衡。

该图来自：刘胥影, 吴建鑫, 周志华. 一种基于级联模型的类别不平衡数据分类方法[J]. 南京大学学报:自然科学版, 2006, 42(2):148-155