简单易学的机器学习算法——K-Means++算法

一、K-Means算法存在的问题

由于K-Means算法的简单且易于实现，因此K-Means算法得到了很多的应用，但是从K-Means算法的过程中发现，K-Means算法中的聚类中心的个数k需要事先指定，这一点对于一些未知数据存在很大的局限性。其次，在利用K-Means算法进行聚类之前，需要初始化k个聚类中心，在上述的K-Means算法的过程中，使用的是在数据集中随机选择最大值和最小值之间的数作为其初始的聚类中心，但是聚类中心选择不好，对于K-Means算法有很大的影响。对于如下的数据集：

如选取的个聚类中心为：

最终的聚类结果为：

为了解决因为初始化的问题带来K-Means算法的问题，改进的K-Means算法，即K-Means++算法被提出，K-Means++算法主要是为了能够在聚类中心的选择过程中选择较优的聚类中心。

二、K-Means++算法的思路

K-Means++算法在聚类中心的初始化过程中的基本原则是使得初始的聚类中心之间的相互距离尽可能远，这样可以避免出现上述的问题。K-Means++算法的初始化过程如下所示：

在数据集中随机选择一个样本点作为第一个初始化的聚类中心

选择出其余的聚类中心：

计算样本中的每一个样本点与已经初始化的聚类中心之间的距离，并选择其中最短的距离，记为d_i

以概率选择距离最大的样本作为新的聚类中心，重复上述过程，直到k个聚类中心都被确定

对k个初始化的聚类中心，利用K-Means算法计算最终的聚类中心。

在上述的K-Means++算法中可知K-Means++算法与K-Means算法最本质的区别是在k个聚类中心的初始化过程。

Python实现：

一、K-Means算法存在的问题

由于K-Means算法的简单且易于实现，因此K-Means算法得到了很多的应用，但是从K-Means算法的过程中发现，K-Means算法中的聚类中心的个数k需要事先指定，这一点对于一些未知数据存在很大的局限性。其次，在利用K-Means算法进行聚类之前，需要初始化k个聚类中心，在上述的K-Means算法的过程中，使用的是在数据集中随机选择最大值和最小值之间的数作为其初始的聚类中心，但是聚类中心选择不好，对于K-Means算法有很大的影响。对于如下的数据集：

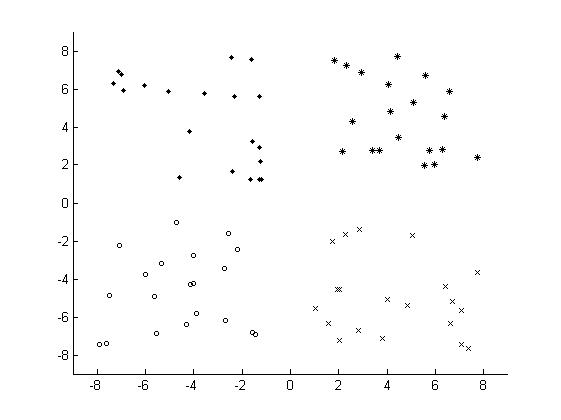
如选取的个聚类中心为：

最终的聚类结果为：

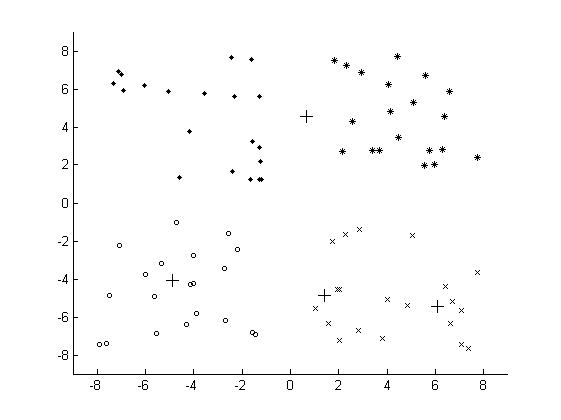
为了解决因为初始化的问题带来K-Means算法的问题，改进的K-Means算法，即K-Means++算法被提出，K-Means++算法主要是为了能够在聚类中心的选择过程中选择较优的聚类中心。

二、K-Means++算法的思路

K-Means++算法在聚类中心的初始化过程中的基本原则是使得初始的聚类中心之间的相互距离尽可能远，这样可以避免出现上述的问题。K-Means++算法的初始化过程如下所示：

在数据集中随机选择一个样本点作为第一个初始化的聚类中心

选择出其余的聚类中心：

计算样本中的每一个样本点与已经初始化的聚类中心之间的距离，并选择其中最短的距离，记为d_i

以概率选择距离最大的样本作为新的聚类中心，重复上述过程，直到k个聚类中心都被确定

对k个初始化的聚类中心，利用K-Means算法计算最终的聚类中心。

在上述的K-Means++算法中可知K-Means++算法与K-Means算法最本质的区别是在k个聚类中心的初始化过程。

Python实现：

# coding:UTF-8
'''
Date:20160923
@author: zhaozhiyong
'''

import numpy as np
from random import random
from KMeans import load_data, kmeans, distance, save_result

FLOAT_MAX = 1e100 # 设置一个较大的值作为初始化的最小的距离

def nearest(point, cluster_centers):
    min_dist = FLOAT_MAX
    m = np.shape(cluster_centers)[0]  # 当前已经初始化的聚类中心的个数
    for i in xrange(m):
        # 计算point与每个聚类中心之间的距离
        d = distance(point, cluster_centers[i, ])
        # 选择最短距离
        if min_dist > d:
            min_dist = d
    return min_dist

def get_centroids(points, k):
    m, n = np.shape(points)
    cluster_centers = np.mat(np.zeros((k , n)))
    # 1、随机选择一个样本点为第一个聚类中心
    index = np.random.randint(0, m)
    cluster_centers[0, ] = np.copy(points[index, ])
    # 2、初始化一个距离的序列
    d = [0.0 for _ in xrange(m)]

    for i in xrange(1, k):
        sum_all = 0
        for j in xrange(m):
            # 3、对每一个样本找到最近的聚类中心点
            d[j] = nearest(points[j, ], cluster_centers[0:i, ])
            # 4、将所有的最短距离相加
            sum_all += d[j]
        # 5、取得sum_all之间的随机值
        sum_all *= random()
        # 6、获得距离最远的样本点作为聚类中心点
        for j, di in enumerate(d):
            sum_all -= di
            if sum_all > 0:
                continue
            cluster_centers[i] = np.copy(points[j, ])
            break
    return cluster_centers

if __name__ == "__main__":
    k = 4#聚类中心的个数
    file_path = "data.txt"
    # 1、导入数据
    print "---------- 1.load data ------------"
    data = load_data(file_path)
    # 2、KMeans++的聚类中心初始化方法
    print "---------- 2.K-Means++ generate centers ------------"
    centroids = get_centroids(data, k)
    # 3、聚类计算
    print "---------- 3.kmeans ------------"
    subCenter = kmeans(data, k, centroids)
    # 4、保存所属的类别文件
    print "---------- 4.save subCenter ------------"
    save_result("sub_pp", subCenter)
    # 5、保存聚类中心
    print "---------- 5.save centroids ------------"
    save_result("center_pp", centroids)

其中，KMeans所在的文件为：

# coding:UTF-8
'''
Date:20160923
@author: zhaozhiyong
'''
import numpy as np

def load_data(file_path):
    f = open(file_path)
    data = []
    for line in f.readlines():
        row = []  # 记录每一行
        lines = line.strip().split("\t")
        for x in lines:
            row.append(float(x)) # 将文本中的特征转换成浮点数
        data.append(row)
    f.close()
    return np.mat(data)

def distance(vecA, vecB):
    dist = (vecA - vecB) * (vecA - vecB).T
    return dist[0, 0]

def randCent(data, k):
    n = np.shape(data)[1]  # 属性的个数
    centroids = np.mat(np.zeros((k, n)))  # 初始化k个聚类中心
    for j in xrange(n):  # 初始化聚类中心每一维的坐标
        minJ = np.min(data[:, j])
        rangeJ = np.max(data[:, j]) - minJ
        # 在最大值和最小值之间随机初始化
        centroids[:, j] = minJ * np.mat(np.ones((k , 1))) + np.random.rand(k, 1) * rangeJ
    return centroids

def kmeans(data, k, centroids):
    m, n = np.shape(data) # m：样本的个数，n：特征的维度
    subCenter = np.mat(np.zeros((m, 2)))  # 初始化每一个样本所属的类别
    change = True  # 判断是否需要重新计算聚类中心
    while change == True:
        change = False  # 重置
        for i in xrange(m):
            minDist = np.inf  # 设置样本与聚类中心之间的最小的距离，初始值为争取穷
            minIndex = 0  # 所属的类别
            for j in xrange(k):
                # 计算i和每个聚类中心之间的距离
                dist = distance(data[i, ], centroids[j, ])
                if dist < minDist:
                    minDist = dist
                    minIndex = j
            # 判断是否需要改变
            if subCenter[i, 0] <> minIndex:  # 需要改变
                change = True
                subCenter[i, ] = np.mat([minIndex, minDist])
        # 重新计算聚类中心
        for j in xrange(k):
            sum_all = np.mat(np.zeros((1, n)))
            r = 0  # 每个类别中的样本的个数
            for i in xrange(m):
                if subCenter[i, 0] == j:  # 计算第j个类别
                    sum_all += data[i, ]
                    r += 1
            for z in xrange(n):
                try:
                    centroids[j, z] = sum_all[0, z] / r
                except:
                    print " r is zero"   
    return subCenter

def save_result(file_name, source):
    m, n = np.shape(source)
    f = open(file_name, "w")
    for i in xrange(m):
        tmp = []
        for j in xrange(n):
            tmp.append(str(source[i, j]))
        f.write("\t".join(tmp) + "\n")
    f.close()

最终的结果为：