python实现斐波那契数列的方法示例

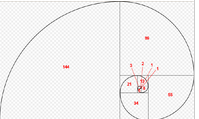
斐波那契数列，又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、……在数学上，斐波纳契数列以如下递归的方法定义：
F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*） 。

1. 元组实现 
fibs = [0, 1]
for i in range(8):
 fibs.append(fibs[-2] + fibs[-1])
这能得到一个在指定范围内的斐波那契数列的列表。
2. 迭代器实现   
class Fibs:
 def __init__(self):
  self.a = 0
  self.b = 1
 
 def next(self):
  self.a, self.b = self.b, self.a + self.b
  return self.a
 
 def __iter__(self):
  return self
这将得到一个无穷的数列，可以采用如下方式访问： 
fibs = Fibs()
for f in fibs:
 if f > 1000:
  print f
  break
 else:
  print f
3. 通过定制类实现
class Fib(object):
 def __getitem__(self, n):
  if isinstance(n, int):
   a, b = 1, 1
   for x in range(n):
    a, b = b, a + b
   return a
  elif isinstance(n, slice):
   start = n.start
   stop = n.stop
   a, b = 1, 1
   L = []
   for x in range(stop):
    if x >= start:
     L.append(a)
    a, b = b, a + b
   return L
  else:
   raise TypeError("Fib indices must be integers")
这样可以得到一个类似于序列的数据结构，可以通过下标来访问数据：
f = Fib()
print f[0:5]
print f[:10]
4.Python实现比较简易的斐波那契数列示例
先放一个斐波那契数列出来瞧瞧…  
0 1 1 2 3 5 8 13 21 34 55 89 144 233...
首先给头两个变量赋值：   
i, j = 0, 1

当然也可以这样写：   
i = 0
j = 1
接着定个范围，就10000之内好了：
while i < 10000:
然后在while语句中输出i并设计逻辑：  
print i,
i, j = j, i+j

在这里需要注意：“i, j = i, i+j”这条代码不能写成如下所示： 
i = j
j = i+j

如果写成这样，j就不是前两位相加的值，而是已经被j赋过值的i和j相加的值，这样的话输出的数列会如下所示：

0 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192

正确的整片代码如下所示： 
i, j = 0, 1
while i < 10000:
 print i,
 i, j = j, i+j

最后展示运行结果：   

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

总结

以上就是关于利用Python实现斐波那契数列的全部内容了，希望本文的内容对大家的学习或者工作能带来一定的帮助，如果有疑问大家可以留言交流。