 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
在实证研究中,层次回归分析是探究“不同变量组对因变量的增量解释力”的核心方法——通过分步骤引入自变量(如先引入人口统计学变量,再引入心理特质变量),观察模型R²的变化、F检验显著性及回归系数,判断新增变量组的价值。但操作中最易困惑的问题之一是:自变量是否需要转换为标准分(Z分数)?
答案并非“绝对需要”或“绝对不需要”,而是取决于研究目标、变量特征及结果解读需求。本文将从层次回归的核心逻辑切入,结合标准分的本质作用,分场景明确标准化的适用边界,通过实战案例对比标准化前后的结果差异,最终形成“按需选择”的决策框架。
要判断是否需要标准化,需先厘清层次回归的分析目标与标准分的核心作用——二者的匹配度直接决定标准化的必要性。
层次回归的核心价值并非仅构建预测模型,而是回答三个关键问题:
新增变量组是否能显著提升模型的解释力?(通过R²变化量及对应的F检验判断);
在控制前序变量的基础上,新增变量对因变量的独立影响如何?(通过新增变量的回归系数显著性判断);
不同变量(或变量组)对因变量的相对重要性如何?(通过系数大小或标准化系数对比)。
其中,前两个问题与变量是否标准化无关,但第三个问题直接依赖标准化操作——这是判断是否需要标准化的关键锚点。
标准分(Z分数)的计算公式为:Z = (X - μ) / σ,其中μ为变量均值,σ为标准差。其核心作用是将不同量纲、不同量级的变量转换为“均值为0、标准差为1”的标准化变量,实现两个关键价值:
消除量纲影响:例如“年龄(岁,范围20-60)”与“月收入(元,范围3000-50000)”,未标准化时,收入的系数绝对值可能远大于年龄,但若二者标准化后,系数可直接对比重要性;
明确系数含义:标准化系数(Beta值)表示“自变量每变化1个标准差,因变量变化的标准差数”,而未标准化系数(B值)表示“自变量每变化1个原始单位,因变量变化的原始单位数”。
层次回归中变量是否标准化,核心取决于“研究是否需要比较变量的相对重要性”及“自变量的量纲特征”,可分为“必须标准化”“建议标准化”“无需标准化”三大场景。
当研究目标包含“判断不同变量(或不同层次变量)对因变量的相对贡献”时,标准化是唯一可行的选择——未标准化系数因量纲差异,完全不具备可比性。
典型研究场景包括:
多维度影响因素分析:如“消费者购买意愿”的影响因素研究,自变量涵盖“价格敏感度(1-7分量表)”“品牌认知(1-10分量表)”“月消费额(元)”,需判断哪个因素对购买意愿的影响更大;
跨层次变量比较:如层次回归中,第一层引入“人口统计学变量(年龄:岁,学历:分类编码)”,第二层引入“心理变量(自我效能感:1-5分)”,需比较两类变量组的相对重要性;
调节效应与中介效应分析:当层次回归用于检验调节效应(如“收入调节价格敏感度对购买意愿的影响”)时,交互项的构建需基于标准化变量,否则交互项会受原始变量量纲影响,导致调节效应判断偏差。
核心逻辑:相对重要性的比较依赖“统一尺度”,标准分正是通过消除量纲实现这一目标。此时若不标准化,可能得出“收入(系数1.2)比价格敏感度(系数0.8)影响更大”的错误结论,实则可能是收入的原始单位(元)量级远大于量表单位。
即使研究不直接比较变量重要性,但当自变量的量纲差异极大时(如“身高:厘米”与“家庭年收入:万元”),未标准化系数的“数值大小”会严重偏离直观认知,增加结果解读难度,此时建议标准化。
例如:在“青少年学业成绩(分)”的层次回归中,第一层引入“家庭年收入(万元,范围5-50)”,第二层引入“每日学习时长(小时,范围1-10)”。未标准化时可能得到:
家庭年收入系数B=0.3(表示年收入每增加1万元,学业成绩增加0.3分);
每日学习时长系数B=2.5(表示学习时长每增加1小时,学业成绩增加2.5分)。
虽无需比较相对重要性,但0.3与2.5的数值差异易让读者误解“学习时长影响远大于收入”,而标准化后得到Beta值(如收入Beta=0.2,学习时长Beta=0.3),可更清晰地反映“两者均为正向影响,且学习时长的标准化影响略大”,解读更直观。
当满足以下任一条件时,变量无需标准化,直接使用原始数据即可,标准化反而会增加“原始意义解读”的成本:
自变量量纲完全一致:如所有自变量均为“1-7分量表”(如满意度、态度量表),或均为“百分比”(如市场占有率、增长率),此时未标准化系数可直接对比,量纲无干扰;
研究仅关注“预测准确性”与“增量解释力”:如工业场景中,通过层次回归预测“设备故障概率”,自变量为“温度(℃)”“压力(MPa)”“运行时长(小时)”,核心目标是判断新增“运行时长”是否提升预测精度,而非比较三个变量的重要性——此时未标准化系数可直接用于预测公式,更贴合实际业务场景;
分类变量(哑变量):分类变量(如性别:0=男,1=女;学历:1=本科,2=硕士)的编码本身无“量纲”概念,标准化无实际意义,直接使用原始编码即可(注意:哑变量需以某一类别为参照组)。
注意:分类变量的“标准化误区”——部分研究者会将哑变量一同标准化,这是错误操作。哑变量的0/1编码代表“是否属于某类别”,标准化后的值(如Z=-0.5, Z=0.5)会丢失原始分类意义,导致系数解读混乱。
以“员工工作绩效(分,因变量)”的层次回归分析为例,清晰展示标准化与否的结果差异。研究设计:
第一层(控制变量):年龄(岁,25-50)、学历(哑变量,1=本科,2=硕士,3=博士);
第二层(核心变量):工作投入(1-7分量表)、月加班时长(小时,0-20);
研究目标:判断核心变量组是否显著提升解释力,并比较核心变量的相对重要性。
分类变量(学历)不标准化,连续变量(年龄、工作投入、加班时长)按Z分数标准化,公式实现(Python):
import pandas as pd
from sklearn.preprocessing import StandardScaler
# 加载数据
data = pd.read_csv("employee_performance.csv")
# 连续变量列表
continuous_vars = ["年龄", "工作投入", "月加班时长"]
# 标准化器
scaler = StandardScaler()
# 生成标准化变量(命名加"_z"区分)
data[continuous_vars] = scaler.fit_transform(data[continuous_vars])
data.rename(columns={col: col+"_z" for col in continuous_vars}, inplace=True)
| 变量 | 未标准化结果(B值±标准误) | 标准化结果(Beta值±标准误) | 显著性(p值) | 结果解读差异 |
|---|---|---|---|---|
| 第一层:控制变量 | - | - | - | - |
| 年龄 | 0.12±0.05 | 0.15±0.06 | 0.02(显著) | 未标准化:年龄每增1岁,绩效增0.12分;标准化:年龄每增1个标准差,绩效增0.15个标准差 |
| 学历(硕士vs本科) | 3.20±1.10 | 0.21±0.07 | 0.004(显著) | 分类变量标准化无意义,Beta值仅为计算结果,解读以B值为主(硕士比本科绩效高3.2分) |
| 第二层:核心变量 | - | - | - | 核心变量组R²变化=0.18,F=23.5,p<0.001,增量解释显著 |
| 工作投入 | 1.50±0.20 | 0.35±0.04 | <0.001(显著) | 未标准化:投入每增1分,绩效增1.5分;标准化:投入每增1个标准差,绩效增0.35个标准差 |
| 月加班时长 | 0.45±0.12 | 0.18±0.03 | <0.001(显著) | 未标准化:加班每增1小时,绩效增0.45分;标准化:加班每增1个标准差,绩效增0.18个标准差 |
增量解释力判断:标准化与否不影响R²变化量(均为0.18)及F检验结果(均显著),说明“新增变量组是否有效”与标准化无关;
相对重要性比较:仅标准化后可判断“工作投入(Beta=0.35)对绩效的影响大于月加班时长(Beta=0.18)”,未标准化时1.5与0.45的差异因量纲(量表分vs小时)无法直接对比;
分类变量解读:学历的Beta值无实际意义,需回归到未标准化B值解读“类别差异”,体现“分类变量无需标准化”的原则。
若确定需要标准化,需掌握“正确的操作流程”与“结果解读规范”,避免因操作不当导致结果偏差。
核心原则:连续变量可标准化,分类变量(含哑变量)绝对不标准化。具体操作步骤:
变量区分:将自变量分为“连续变量”(如年龄、收入、量表得分)与“分类变量”(如性别、学历、职业);
分类变量处理:对无序分类变量(如职业)做哑变量编码,有序分类变量(如学历)按等级编码(1、2、3...),均保留原始编码;
连续变量标准化:仅对连续变量计算Z分数,生成新的标准化变量(命名建议加“_z”后缀,如“年龄_z”);
模型构建:将“分类变量+标准化连续变量”代入层次回归模型,按研究设计分层次引入变量。
1. 转换→计算变量:
目标变量:年龄_z
数字表达式:(年龄 - MEAN(年龄)) / SD(年龄)
(重复操作,生成所有连续变量的标准分)
2. 分析→回归→线性:
第一层:移入分类变量(学历)+ 标准化连续变量(年龄_z)
第二层:追加标准化连续变量(工作投入_z、加班时长_z)
(勾选“统计量”中的“R方变化”“共线性诊断”)
3. 结果读取:输出表中“标准化系数Beta”即为核心解读指标
import statsmodels.api as sm
from sklearn.preprocessing import StandardScaler
# 1. 数据准备与标准化
data = pd.read_csv("employee_performance.csv")
# 分类变量(学历)编码
data["学历_硕士"] = (data["学历"] == 2).astype(int)
data["学历_博士"] = (data["学历"] == 3).astype(int)
# 连续变量标准化
scaler = StandardScaler()
continuous_vars = ["年龄", "工作投入", "月加班时长"]
data[continuous_vars] = scaler.fit_transform(data[continuous_vars])
# 2. 层次回归:第一层(控制变量)
X1 = data[["年龄", "学历_硕士", "学历_博士"]] # 年龄已标准化
X1 = sm.add_constant(X1) # 加入常数项
y = data["工作绩效"]
model1 = sm.OLS(y, X1).fit()
# 3. 层次回归:第二层(加入核心变量)
X2 = data[["年龄", "学历_硕士", "学历_博士", "工作投入", "月加班时长"]]
X2 = sm.add_constant(X2)
model2 = sm.OLS(y, X2).fit()
# 4. 结果输出:对比R²变化与标准化系数
print("第一层R²:", model1.rsquared)
print("第二层R²:", model2.rsquared)
print("R²变化量:", model2.rsquared - model1.rsquared)
print("n标准化系数(Beta):")
print(pd.DataFrame({
"变量": X2.columns[1:], # 排除常数项
"Beta值": model2.params[1:],
"p值": model2.pvalues[1:]
}).round(3))
标准化后的层次回归结果需区分“连续变量”与“分类变量”,采用不同指标解读:
连续变量:优先解读Beta值(相对重要性),辅以B值(原始单位影响)。例如“工作投入_z的Beta=0.35,p<0.001”,解读为“控制年龄、学历后,工作投入每增加1个标准差,工作绩效显著增加0.35个标准差,是核心影响因素”;
分类变量:仅解读未标准化B值,Beta值可忽略。例如“学历_硕士的B=3.2,p=0.004”,解读为“控制其他变量后,硕士学历员工的工作绩效比本科学历显著高3.2分”;
增量解释力:直接对比两层模型的R²变化量及对应的F检验p值,若p<0.05,说明新增变量组显著提升解释力。
错误操作:将性别(0/1)、学历(1/2/3)等分类变量与连续变量一同标准化;
后果:分类变量的标准化值丢失“类别属性”,如性别标准化后可能为-0.5(男)和0.5(女),系数解读变为“性别每增加1个标准差,绩效变化X”,完全脱离业务逻辑;
避坑:分类变量仅做编码(哑变量/等级编码),不参与标准化。
错误认知:标准化后模型的R²、F检验结果会变化,影响预测准确性;
事实:标准化仅改变变量的“尺度”,不改变变量间的线性关系,因此模型的R²、调整R²、F检验结果、p值完全不变,仅回归系数的数值发生变化;
避坑:放心标准化,核心拟合指标不受影响,仅需调整系数解读方式。
错误案例:自变量“月收入(万元,B=0.8)”与“满意度(量表,B=0.5)”,认为收入影响更大;
后果:忽略量纲差异导致结论偏差——若收入标准差为10万元,满意度标准差为2分,标准化后收入Beta=0.8×10/绩效标准差,满意度Beta=0.5×2/绩效标准差,实际可能满意度影响更大;
避坑:只要变量量纲不同,比较重要性必须用标准化系数。
错误认知:标准化后变量的层次引入顺序需要调整;
事实:层次顺序由研究理论决定(如先控制人口学变量,再引入核心变量),与变量是否标准化无关;
避坑:先明确理论框架确定变量层次,再决定是否对连续变量标准化。
层次回归中变量是否需要标准化,本质是“研究目标”与“变量特征”的匹配问题,无需绝对化。最终可通过以下决策逻辑图快速判断:
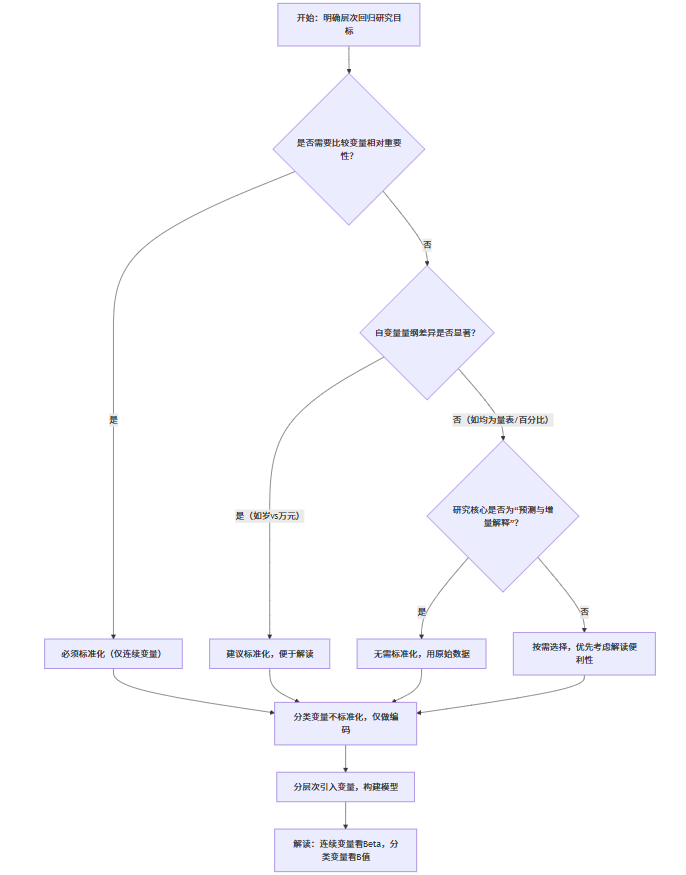
核心结论:层次回归的标准化不是“必选项”,而是“按需选项”——当研究涉及“相对重要性比较”或“变量量纲差异大”时,标准化是提升结果解读价值的关键操作;当变量量纲一致且仅关注预测效果时,原始数据更贴合业务场景。无论选择哪种方式,清晰的研究目标与规范的结果解读,远比“是否标准化”本身更重要。


数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
第一章:数据分析思维考点1:UVCA时代的特点考点2:数据分析背后的逻辑思维方法论考点3:流程化企业的数据分析需求考点4:企业数 ...
2026-02-16在数据分析、业务决策、科学研究等领域,统计模型是连接原始数据与业务价值的核心工具——它通过对数据的规律提炼、变量关联分析 ...
2026-02-14在SQL查询实操中,SELECT * 与 SELECT 字段1, 字段2,...(指定个别字段)是最常用的两种查询方式。很多开发者在日常开发中,为了 ...
2026-02-14对CDA(Certified Data Analyst)数据分析师而言,数据分析的核心不是孤立解读单个指标数值,而是构建一套科学、完整、贴合业务 ...
2026-02-14在Power BI实操中,函数是实现数据清洗、建模计算、可视化呈现的核心工具——无论是简单的数据筛选、异常值处理,还是复杂的度量 ...
2026-02-13在互联网运营、产品迭代、用户增长等工作中,“留存率”是衡量产品核心价值、用户粘性的核心指标——而次日留存率,作为留存率体 ...
2026-02-13对CDA(Certified Data Analyst)数据分析师而言,指标是贯穿工作全流程的核心载体,更是连接原始数据与业务洞察的关键桥梁。CDA ...
2026-02-13在机器学习建模实操中,“特征选择”是提升模型性能、简化模型复杂度、解读数据逻辑的核心步骤——而随机森林(Random Forest) ...
2026-02-12在MySQL数据查询实操中,按日期分组统计是高频需求——比如统计每日用户登录量、每日订单量、每日销售额,需要按日期分组展示, ...
2026-02-12对CDA(Certified Data Analyst)数据分析师而言,描述性统计是贯穿实操全流程的核心基础,更是从“原始数据”到“初步洞察”的 ...
2026-02-12备考CDA的小伙伴,专属宠粉福利来啦! 不用拼运气抽奖,不用复杂操作,只要转发CDA真题海报到朋友圈集赞,就能免费抱走实用好礼 ...
2026-02-11在数据科学、机器学习实操中,Anaconda是必备工具——它集成了Python解释器、conda包管理器,能快速搭建独立的虚拟环境,便捷安 ...
2026-02-11在Tableau数据可视化实操中,多表连接是高频操作——无论是将“产品表”与“销量表”连接分析产品销量,还是将“用户表”与“消 ...
2026-02-11在CDA(Certified Data Analyst)数据分析师的实操体系中,统计基本概念是不可或缺的核心根基,更是连接原始数据与业务洞察的关 ...
2026-02-11在数字经济飞速发展的今天,数据已成为核心生产要素,渗透到企业运营、民生服务、科技研发等各个领域。从个人手机里的浏览记录、 ...
2026-02-10在数据分析、实验研究中,我们经常会遇到小样本配对数据的差异检验场景——比如同一组受试者用药前后的指标对比、配对分组的两组 ...
2026-02-10在结构化数据分析领域,透视分析(Pivot Analysis)是CDA(Certified Data Analyst)数据分析师最常用、最高效的核心实操方法之 ...
2026-02-10在SQL数据库实操中,字段类型的合理设置是保证数据运算、统计准确性的基础。日常开发或数据分析时,我们常会遇到这样的问题:数 ...
2026-02-09在日常办公数据分析中,Excel数据透视表是最常用的高效工具之一——它能快速对海量数据进行分类汇总、分组统计,将杂乱无章的数 ...
2026-02-09表结构数据作为结构化数据的核心载体,其“获取-加工-使用”全流程,是CDA(Certified Data Analyst)数据分析师开展专业工作的 ...
2026-02-09