 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
在神经网络模型设计中,隐藏层神经元个数的确定是影响模型性能、训练效率与泛化能力的关键环节。本文从神经网络的基础结构出发,系统梳理隐藏层神经元个数确定的核心方法,包括经验公式法、实验调整法、自适应优化法等,结合不同任务场景分析影响神经元个数选择的关键因素,并通过实际案例验证方法的有效性,同时指出常见认知误区,为工程师与研究者提供可落地的神经元个数设计指南。
典型的神经网络由输入层、隐藏层与输出层构成。输入层负责接收原始数据(如图像像素、文本特征),输出层输出模型预测结果(如分类标签、回归值),而隐藏层则通过非线性变换提取数据的深层特征 —— 这一 “特征提取” 能力的强弱,直接取决于隐藏层的层数与每层神经元的个数。
隐藏层神经元个数的选择存在 “Goldilocks 困境”:
个数过少:模型表达能力不足,无法捕捉数据中的复杂规律,易出现 “欠拟合”,表现为训练集与测试集误差均较高;
个数过多:模型复杂度超出数据需求,易记忆训练集中的噪声,导致 “过拟合”,表现为训练集误差低但测试集误差骤升;
个数不合理:还会增加训练时间(如参数更新次数增多、梯度消失风险上升),浪费计算资源(如内存占用过高)。
因此,科学确定隐藏层神经元个数,是平衡模型性能、效率与泛化能力的核心前提。
经验公式基于输入层、输出层神经元个数与数据特性,为隐藏层神经元个数提供初始参考范围,适用于模型设计的初步阶段。以下为工业界常用公式及适用场景:
| 经验公式 | 公式表达式(为隐藏层神经元个数,为输入层个数,为输出层个数,为样本数量) | 适用场景 | 优缺点 |
|---|---|---|---|
| 基础比例法 | (为 1-10 的调整系数) | 简单任务(如线性分类、小规模回归) | 计算简单,适合快速初始化;忽略数据复杂度,精度有限 |
| 数据规模法 | 或 | 样本量较小()的场景 | 考虑数据量对泛化能力的影响;样本量过大时估算值偏保守 |
| 复杂度适配法 | 或 | 中等复杂度任务(如文本分类、简单图像识别) | 平衡输入输出层影响,适配多数传统机器学习任务;对深度学习复杂任务适用性弱 |
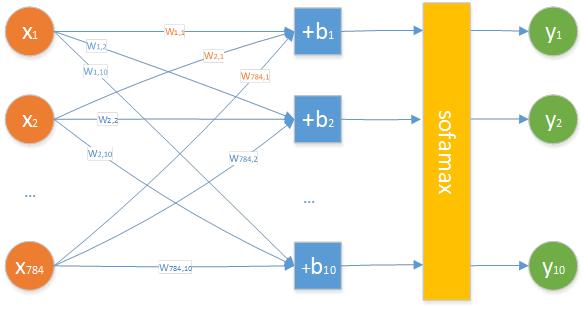
注意:经验公式的结果仅为 “初始值”,需结合后续实验调整,不可直接作为最终值。例如,在手写数字识别任务中(输入层 784 个神经元,输出层 10 个),按基础比例法计算得 ,可将 80-100 作为神经元个数的初始搜索范围。
实验调整法通过 “控制变量 + 性能验证” 的方式,在经验公式的基础上找到最优神经元个数,是工业界最常用的落地方法,核心步骤如下:
以经验公式估算值为中心,设定合理的搜索范围(如估算值 ±50%)与步长(如步长为 10 或 20,避免搜索效率过低)。例如,若初始估算值为 80,可设定搜索范围为 40-120,步长为 20。
对每个候选神经元个数,采用 k 折交叉验证(通常 k=5 或 10)训练模型,评估指标需覆盖 “拟合程度”(如训练集准确率、MSE)与 “泛化能力”(如测试集准确率、交叉验证均值),同时记录训练时间与内存占用。
绘制 “神经元个数 - 性能指标” 曲线,选择 “测试集性能最高、训练效率可接受” 的点作为最优值。例如,在某文本分类任务中,当神经元个数从 40 增至 80 时,测试集 F1 分数从 0.82 升至 0.89;继续增至 120 时,F1 分数仅提升 0.01,但训练时间增加 40%,此时 80 即为最优值。
随着自动机器学习(AutoML)的发展,自适应优化法通过算法自动搜索最优神经元个数,减少人工干预,适用于复杂模型(如深度神经网络、Transformer 子网络):
网格搜索:遍历预设的所有神经元个数组合(如隐藏层 1:[60,80,100],隐藏层 2:[30,40,50]),适合小范围精细搜索;
随机搜索:在搜索范围内随机采样候选值,适合大范围快速探索,实验表明其在高维空间中效率优于网格搜索。
基于贝叶斯定理构建 “神经元个数 - 性能” 的概率模型,每次迭代根据历史实验结果,优先选择 “可能带来性能提升” 的候选值,大幅减少搜索次数。例如,在 CNN 图像分类任务中,贝叶斯优化可将神经元个数搜索次数从 50 次降至 15 次,同时找到更优值。
模拟生物进化过程(选择、交叉、变异),将神经元个数作为 “基因” 构建种群,通过多代迭代筛选出性能最优的 “个体”。该方法适用于多隐藏层模型,可同时优化各层神经元个数(如隐藏层 1 与隐藏层 2 的个数组合)。
数据维度:高维数据(如高清图像、长文本)需更多神经元捕捉特征,例如 224×224 图像的输入层(50176 个神经元)对应的隐藏层个数,通常比 28×28 图像(784 个神经元)多 2-3 倍;
数据分布:非结构化数据(如语音、视频)比结构化数据(如表格数据)需更多神经元,因前者特征提取难度更高。
分类任务:类别数越多,输出层个数越多,隐藏层个数需相应增加(如 100 类分类任务比 10 类任务的隐藏层个数多 30%-50%);
生成任务(如 GAN、VAE):需更多神经元构建复杂的生成模型,例如 GAN 的生成器隐藏层神经元个数通常比判别器多 50% 以上。
隐藏层层数:多层隐藏层(深度网络)可减少单层神经元个数,例如 “2 层隐藏层(各 80 个神经元)” 的性能可能优于 “1 层隐藏层(160 个神经元)”,且更易训练;
特殊层设计:含卷积层、池化层的 CNN,全连接隐藏层的神经元个数可大幅减少(因卷积层已完成特征降维);含注意力机制的 Transformer,隐藏层神经元个数需与注意力头数匹配(如头数为 8 时,神经元个数通常为 512 或 1024,需被 8 整除)。
若采用强正则化方法(如 Dropout 率 0.5、L2 正则化系数较大),可适当增加神经元个数 —— 正则化可抑制过拟合,而更多神经元能提升模型表达能力。例如,在使用 Dropout 的文本分类任务中,隐藏层神经元个数可从 80 增至 120,且无明显过拟合。
数据集:MNIST(60000 张训练图、10000 张测试图,每张 28×28 像素,输入层 784 个神经元,输出层 10 个神经元);
模型:2 层全连接神经网络(隐藏层 1 + 隐藏层 2);
目标:确定两层隐藏层的最优神经元个数,使测试集准确率≥98%,训练时间≤30 分钟。
隐藏层 1 初始值:按基础比例法 ,设定范围 60-120;
隐藏层 2 初始值:按数据规模法 (因多层网络可减少单层个数,调整为 40-80)。
采用贝叶斯优化工具(如 Hyperopt),以 “测试集准确率” 为目标函数,搜索范围:H1∈[60,120],H2∈[40,80],迭代 15 次。
| 隐藏层 1 个数 | 隐藏层 2 个数 | 测试集准确率 | 训练时间 | 结论 |
|---|---|---|---|---|
| 80 | 60 | 98.2% | 22 分钟 | 准确率达标,时间最优 |
| 100 | 70 | 98.3% | 28 分钟 | 准确率略高,时间接近上限 |
| 120 | 80 | 98.3% | 35 分钟 | 准确率无提升,时间超上限 |
最终选择 “隐藏层 1:80 个,隐藏层 2:60 个”,满足性能与效率需求。
规避策略:以 “测试集性能” 而非 “训练集性能” 为核心指标,当神经元个数增加但测试集性能无提升时,立即停止增加;配合正则化方法,平衡表达能力与泛化能力。
规避策略:根据 “特征提取逻辑” 设计不同层数的神经元个数 —— 通常隐藏层从输入到输出呈 “递减” 趋势(如 784→80→60→10),因深层网络需逐步压缩特征维度,减少冗余信息。
规避策略:在确定搜索范围时,先计算参数总量(每个神经元的参数 = 输入维度 + 1,如 80 个神经元的参数 = 784+1=785),确保参数总量不超过硬件内存(如 GPU 内存 8GB 时,参数总量≤1e8)。
随着大模型与自适应架构的兴起,隐藏层神经元个数的确定正从 “人工设计” 向 “自动优化” 演进:
动态架构模型(如 Dynamic Neural Networks)可根据输入数据实时调整神经元个数,避免固定结构的局限性;
预训练模型(如 BERT、ResNet)通过海量数据学习到最优的神经元个数配置,微调阶段仅需小幅调整,减少设计成本;
多目标优化算法(如兼顾准确率、速度、能耗)将成为神经元个数确定的核心方向,适配边缘设备等资源受限场景。
隐藏层神经元个数的确定并非 “一刀切” 的固定规则,而是 “理论指导 + 实验验证 + 场景适配” 的迭代过程:首先通过经验公式确定初始范围,再通过实验调整或自适应优化找到最优值,最终结合数据特性、任务需求与硬件资源验证有效性。未来,随着自动机器学习技术的成熟,神经元个数的设计将更高效、更智能,但工程师仍需理解其核心逻辑,才能在复杂场景中做出合理决策。
[1] Bishop C M. Pattern Recognition and Machine Learning [M]. Springer, 2006.(经典教材,系统阐述神经网络结构设计原理)
[2] Bergstra J, Bengio Y. Random Search for Hyper-Parameter Optimization [J]. Journal of Machine Learning Research, 2012.(随机搜索在超参数优化中的应用)
[3] Snoek J, Larochelle H, Adams R P. Practical Bayesian Optimization of Machine Learning Algorithms [C]. NeurIPS, 2012.(贝叶斯优化的经典论文)


数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在Python面向对象编程(OOP)中,类方法是构建模块化、可复用代码的核心载体,也是实现封装、继承、多态特性的关键工具。无论是 ...
2026-02-27在MySQL数据库优化中,索引是提升查询效率的核心手段—— 面对千万级、亿级数据量,合理创建索引能将查询时间从秒级压缩到毫秒级 ...
2026-02-27在数字化时代,企业积累的海量数据如同散落的珍珠,若缺乏有效的梳理与分类,终将难以发挥实际价值。CDA(Certified Data Analys ...
2026-02-27在问卷调研中,我们常遇到这样的场景:针对同一批调查对象,在不同时间点(如干预前、干预后、随访期)发放相同或相似的问卷,收 ...
2026-02-26在销售管理的实操场景中,“销售机会”是核心抓手—— 从潜在客户接触到最终成交,每一个环节都藏着业绩增长的关键,也暗藏着客 ...
2026-02-26在CDA数据分析师的日常工作中,数据提取、整理、加工是所有分析工作的起点,而“创建表”与“创建视图”,则是数据库操作中最基 ...
2026-02-26在机器学习分析、数据决策的全流程中,“数据质量决定分析价值”早已成为行业共识—— 正如我们此前在运用机器学习进行分析时强 ...
2026-02-25在数字化时代,数据已成为企业决策、行业升级的核心资产,但海量杂乱的原始数据本身不具备价值—— 只有通过科学的分析方法,挖 ...
2026-02-25在数字化时代,数据已成为企业核心资产,而“数据存储有序化、数据分析专业化、数据价值可落地”,则是企业实现数据驱动的三大核 ...
2026-02-25在数据分析、机器学习的实操场景中,聚类分析与主成分分析(PCA)是两种高频使用的统计与数据处理方法。二者常被用于数据预处理 ...
2026-02-24在聚类分析的实操场景中,K-Means算法因其简单高效、易落地的特点,成为处理无监督分类问题的首选工具——无论是用户画像分层、 ...
2026-02-24数字化浪潮下,数据已成为企业核心竞争力,“用数据说话、用数据决策”成为企业发展的核心逻辑。CDA(Certified Data Analyst) ...
2026-02-24CDA一级知识点汇总手册 第五章 业务数据的特征、处理与透视分析考点52:业务数据分析基础考点53:输入和资源需求考点54:业务数 ...
2026-02-23CDA一级知识点汇总手册 第四章 战略与业务数据分析考点43:战略数据分析基础考点44:表格结构数据的使用考点45:输入数据和资源 ...
2026-02-22CDA一级知识点汇总手册 第三章 商业数据分析框架考点27:商业数据分析体系的核心逻辑——BSC五视角框架考点28:战略视角考点29: ...
2026-02-20CDA一级知识点汇总手册 第二章 数据分析方法考点7:基础范式的核心逻辑(本体论与流程化)考点8:分类分析(本体论核心应用)考 ...
2026-02-18第一章:数据分析思维考点1:UVCA时代的特点考点2:数据分析背后的逻辑思维方法论考点3:流程化企业的数据分析需求考点4:企业数 ...
2026-02-16在数据分析、业务决策、科学研究等领域,统计模型是连接原始数据与业务价值的核心工具——它通过对数据的规律提炼、变量关联分析 ...
2026-02-14在SQL查询实操中,SELECT * 与 SELECT 字段1, 字段2,...(指定个别字段)是最常用的两种查询方式。很多开发者在日常开发中,为了 ...
2026-02-14对CDA(Certified Data Analyst)数据分析师而言,数据分析的核心不是孤立解读单个指标数值,而是构建一套科学、完整、贴合业务 ...
2026-02-14